价格弹性
1.价格弹性的概述

所谓价格弹性,即是需求量对价格的弹性,则指某一产品价格变动时,该种产品需求量相应变动的灵敏度。而价格弹性分析,就是应用弹性原理,就产品需求量对价格变动的反应程度进行分析、计算、预测、决策。
价格弹性表明供求对价格变动的依存关系,反映价格变动所引起的供求的相应的变动率,即供给量和需求量对价格信息的敏感程度,又称供需价格弹性。商品本身的价格、消费者的收入、替代品价格,以及消费者的爱好等因素都会影响对商品消费的需求。价格弹性是指这些因素保持不变的情况下,该商品本身价格的变动引起的需求数量的变动。在需求有弹性的情况下,降价会引起购买量的相应增加,从而使消费者对这种商品的货币支出增加;反之,价格上升则会使消费者对这种商品的货币支出减少。在需求弹性等于1的情况下,降价不会引起消费者对这种商品的货币支出的变动。
价格弹性取决于该商品的替代品的数目及其相关联(即可替代性)的程度、该商品在购买者预算中的重要性和该商品的用途等因素。价格弹性主要应用于企业的决策和政府的经济决策。
2.价格弹性的类型
价格弹性可分为需求价格弹性、供给的价格弹性、交叉价格弹性、预期价格弹性等各种类型。
需求价格弹性是需求变动率与引起其变动的价格变动率的比率,反映商品价格与市场消费容量的关系,表明价格升降时需求量的增减程度,通常用需求量变动的百分数与价格变动的百分数的比率来表示,也可做图或列表示之;
供给价格弹性是供给变动率与引起其变动的价格变动率的比率,反映价格与生产量的关系,表明价格升降时供给量的增减程度,通常用供给量变动百分数与价格变动百分数的比率衡量;
交叉价格弹性又称交错价格弹性,是需求的变动率与替代品或补充品价格变动率的比率,表明某商品价格变动对另一商品需求量的影响程度;
预期价格弹性是价格预期变动率与引起这种变动的当前价格变动率的比率,反映未来价格变动对当前价格的影响,用预期的未来价格的相对变动与当前价格的相对变动的比例表示。
3.价格弹性的几何理解[1]
对点弹性而言,不妨设需求曲线为Q=Q(P)。式中,P为价格,Q为需求量。此时设Ed表示价格弹性,则有
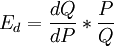
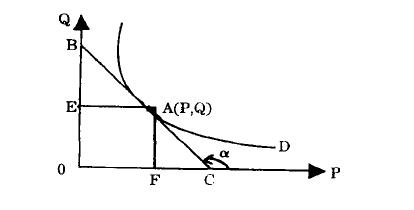
从图中可知:D为需求曲线,其表达式为0=Q(P),点A的坐标为A(P,Q)
过A点的曲线D的切线斜率为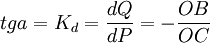 式中,Kd为切线的斜率。
式中,Kd为切线的斜率。
因为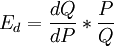 ,
,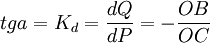 ,A点的坐标为P=AE,Q=AF,P=OE,Q=OF
,A点的坐标为P=AE,Q=AF,P=OE,Q=OF
所以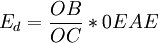
因为△BOS∽△BEA,所以, 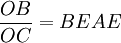
因为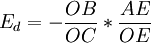 ,
,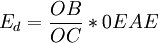 ,所以
,所以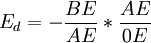
得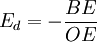
而且因为AE∥0C,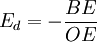 所以
所以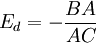 (平行切割)
(平行切割)
显然,D线上任意一点处的弹性是以切点内分上部、下部线段的比值取负号。
4.价格弹性与斜率的关系及应用[1]
从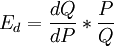 中看出,图中A点切线的斜率是与Ed相关的,但不是同一种概念,即价格弹性不是斜率。
中看出,图中A点切线的斜率是与Ed相关的,但不是同一种概念,即价格弹性不是斜率。
从图中看,当切点位于切线中点时有:|Ed|=1
显然,AB上|Ed|<1,AC上|Ed|>1。
这样,即使是同一条需求曲线D上不同点处的价格弹性均不一样。那么,P处于何处时可降价呢?当价格P位于P>F且接近c的较高部位时,降价可使需求量Q增加;反之,当价格P位于P<F且接近0的较底部位时,降价对需求量的增加将不明显,效果不会理想。
当不需计算Ed的精确值时,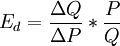 。这时应用可不必知道需求曲线方程即可不知Q=Q(P),只需知道需求曲线两点的价格和需求量即可。
。这时应用可不必知道需求曲线方程即可不知Q=Q(P),只需知道需求曲线两点的价格和需求量即可。
实例1:存在线性关系的某商店,即:Q=Q(P)是线性的。若价格由1元上升到3元,需求量由1000个单位下降到800个单位。求该商品的需求弹性。
解:由题意可得
△Q=800-1000=-200(单位)
△P=3-1=2(元)
Q=1000(单元) P=1(元)
则有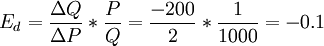
弧弹性公式的应用。
针对Q=Q(P),对P的上升/下降,|Ed|应一致,但基准量Q、P不同,|Ed|将不一致。
实例2:将实例1变化一下可得,P 由3元下降到1元,Q从800单位上升到1000单位,试求 。
解:△Q=1000-800=200(单元)
△P=1-3=-2(元)
Q=1000(单位)P=3(元)
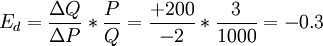
为了不出现上述现象,可用弧弹性公式来进行计算。 首先,看看公式的变化。
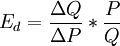
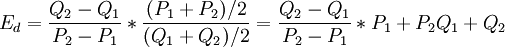
式中,Pl,Ql是基期数据;P2,Q2是报告期数据。这样 便不再会出现P上升或下降的绝对量一致,Q 下降或上升的 绝对量一致, 不一致的问题。
实例3:
对实例1有
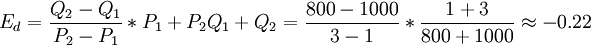
对实例2有
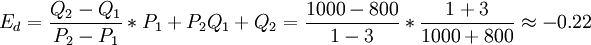
显然,用弧弹性公式结果是一致的。
